建築デッサン原論①パース
このサイトもそろそろ、コンテンツの本筋である受験技術そのものについて、情報の蔵を築いていかねばなるまい。
今回から全3回にわけて、〈建築デッサン原論〉と題し、空間構成ひいては総合表現でモノを描くにあたって理解し・運用できるようになっておくべき原理をできる限り網羅的にまとめる。ゼロから一通り理解したい入門者から、思考を整理したい浪人生まで、迷ったときに参照し、理解の足がかりにしてほしい。
〈建築デッサン原論〉
①パース
③光の反射・屈折
第一回はパース(遠近法)を学ぼう。これはモノの画面上でのかたちを定めるときに使う原理で、知らないと下書きができない。つまり何も描けない。建築科受験生の初歩であり、そして最後まで気の抜けない一つの大きなテーマになる。
建築科ほどパースが肝要になる科はない。一つにはモチーフの問題。主人公は人やお花など自然物ではなく、多く直線や直角で構成された幾何形態である。単純で描きやすいようにも思えるが、普遍的な寸法からズレると明確な"誤り"となるシビアな世界だ。また一つには、目の前にモノがないこと。実空間に立ち現れる形態を想像し"頭で描く"作業では、感覚ではなく理論がものを言う。
"感じるな、考えろ!"
0. パースの原理
さて。"原論"らしく、めちゃくちゃ根本的な話から始めよう。絵とは何か?
ここで言う絵とは写実画のことである。写実画とは、人間の視界を平面に起こしたものに他ならない。空間認識を平面化するにはキュビズム絵画や見取り図の類など様々な表記法があり得るが、人間の視界、すなわち瞳という一点に集まる物体からの光を任意の範囲(25°〜100°ぐらい)切り取って角度によってプロットした表記の再現が、普段そうやって空間を知覚している我々にとっては圧倒的に認識しやすいものなのだ(※当たり前のことを言っています)。で、建築科の試験でも、空間を作るモノの人にとっての感じをわかりやすく伝えたいので、この写実画という形式で平面表記せよというのが暗黙の前提なわけ。

人間の視界の特徴はやっぱり、ある一点(視点)からの角度でプロットするってこと。実際の大きさは違っても角度が同じなら、画面上では全部同じ大きさ。
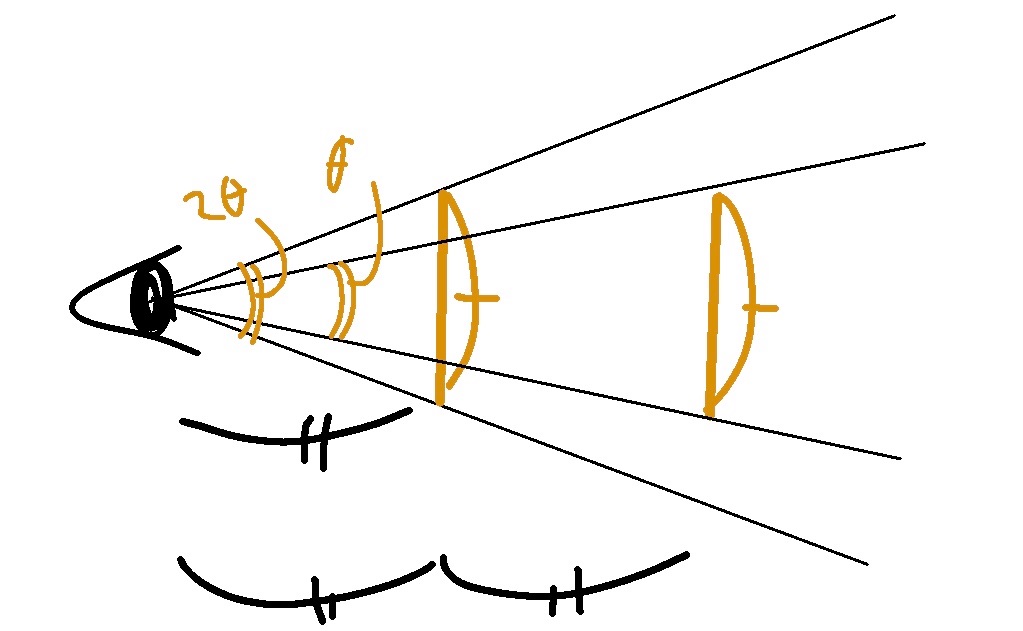
逆に同じ大きさのものも遠くに行くほど画面上では小さくなり、その比率は視点からの距離と反比例する。
言ってしまえばこれが全て。皆さんご存知遠近法、美術の人間はカッコつけて英訳のperspectiveからパースと呼ぶ。

参考:パースのない絵の例(キャビネット図/屏風絵)。無限の遠さから見れば角度の差が無視できるのでこうも見えるはずだが、奥行きの情報がなく空間描写としては弱い。
1. 透視図法
前章の話は、そのまま具体的な描画法につながっていく。

同じ長さの棒の列は、遠ざかるにつれ一定の比率で短くなっていく。すると、その棒を幅とする、空間上では平行な2本の直線は、画面上では徐々に狭まる2直線となる。

それは無限の彼方で一点に交わる。いや、空間上はどこまで行っても幅があるはずだけど、画面上では仮想の一点に漸近する。その点を消失点と呼ぶ。

面白いのは、空間上で平行な直線は全て同じ消失点に収斂するということだ。なぜならそれらの線が平行である限り、その間に同様の比率で短くなっていく棒が描かれるから。例えばこの"道"に車線を増やしてみたり、路端に街灯を生やしてみるとき、はじめの2本と平行な線が見つかる。それらはこの消失点から作図できるだろう。

ところで、隣車線まで行くともはや、道幅の棒の左端より右端のほうが視点から遠いはずだ。・・・ということは?

右に行くほど棒どうしの幅は狭まっていき、同様のことが起きるはずだ。新たな平行線の組に、新たな消失点。
ちなみに、2つの消失点は画面上で同じ高さに来る。もっと言えばその高さは"視点の高さ"と同じになる。なぜか?

"視点の高さ"の平面がある。視点を含む平面は"線"にしか見えないので、この平面上の直線たちの消失点はもちろんその"線"上にある。さらにこれらの消失点には"平面上にはないけど平面上の直線たちに平行な直線たち"も収斂する。結局、とにかく地面に水平な直線たちの消失点は絶対に"視点の高さ"の平面もとい"線"上に来る。この、画面上での視点の高さの線をアイレベル(eye-level)と呼ぶ。地面(これも水平な直線たちの集合である)が見えるのもこのアイレベルまで。仮に地球が丸くなくても、地平線はアイレベルに漸近する。
初習の人は、ここらへん無理に理解する必要はない。一発でわかる奴なんておらん。実際の運用とこういう原理的思考を行き来しながら、だんだんと感覚的に掴めてくるものだ。
ちょっとブレイク。
アイレベルの原理を知っていると、遠目に見ただけでモノの高さがわかるようになる。例えば今この記事を電車内で読んでいるキミは、ちょっと目を上げてみよう。

水平な直線は町のそこら中にあるので、消失点からだいたいのアイレベルを求められる。それと比べて、向こうの人の身長が自分(の厳密には目の高さ)より高いかとか、あるいは自分が屈んでアイレベルを合わせれば、遠くのモノの高さ=その時の目の高さでだいたい測れる。
さて、空間のx軸とy軸の消失点を求めてきたので、z軸でもやってみよう。先の交差点に井戸を掘る。深く行くほど視点から遠くなるから、狭まっていって、そのうち…

そのうち消失点があるはずだ。
ところで消失点の距離は、消失する線どうしの角度に拠るよね。このゆるい/キツイは何で決まるのだろうか?
一つは視線に対する(空間上での)線の角度。浅い角度から見るほうが遠近の差分が大きく、線たちの狭まりは急になる。加えて、全体的なパースのキツさを左右する大事な要因がもう一つ。それは視点からの距離だ。

モノに近づくことによっても、遠近の差が出てパースは急になる。逆に言えばあなたはパースのキツさでもって、そのモノをどれくらい離れて見ているのか表現することになる。没入して迫力を見せたいのか、引いて静的に置きたいのか。考えて操れるといい。
あぁ、ちなみに。消失点の距離の話が出たが、実際に描く時に消失点から作図できることは稀である。なぜならだいたい画面の外に出ちゃうから。近めの外ならまだ練りゴムでも目印に置いとけばいいが、もっと緩やかなパースは基本的に感覚で狭めることになるだろう。感覚に慣れすぎた上級者は逆に、近めの消失点はきちんと作図するように。ボロが出るぞ。
話を戻して、井戸が掘れた。空間の三次元に対応して消失点が3つあるので、この状態を3点透視(図法)と呼ぶ。ここからいずれかの軸に線が無いか、あっても視線とほぼ垂直(→どちらが遠いともつかない)で消失点が省略されると、2点透視、1点透視となっていく。最初の一本道の絵は1点透視で、交差点の絵は2点透視だったね。学校や予備校が大好きな分類だ。
参考:3点透視の例



参考:2点透視の例



参考:1点透視の例



まあでもカテゴリーに囚われる必要はない。xyz軸だけで構成された豆腐近代建築を描くにはそれで良いかもしれないが、消失点なんて視線に垂直でない平行な線の組の数だけあるのだ。典型的な3パターンに収まる場合の方が少ない、くらいに思っていい。


とはいえイレギュラーな線もだいたいxyzで求めた基準点から作図できるもので、次章で扱う円弧も基本的にはそう。究極、立方体が描ければ何でも描ける。
そこで、とにかくあらゆる方向から見た立方体を書けるようになるのが、パースに慣れたい人への宿題。暇な授業でノートの端にでも、色んな角度・視点の距離(∽パースのキツさ)から10個も20個も描いてみる。できれば手元に立方体を置いて見比べる。ハンズとかで小さいのを買って筆箱に入れておくでも、ケント紙で大きめに自作して部屋に置いておくでもいい。プロポーション(形態の比率)の精度を上げ続けよう。なぜかみんな横に太りがちだから、紙を回転させてチェック!合格者でも怪しいのを描いたりするから、終わりはない。
https://twitter.com/yuassamakoto/status/805790041750392832?s=21
立方体を正確に描く練習と、フリーハンドで長くまっすぐな線を引く練習は建築科の古典的筋トレ。日課にして信奉していた合格者も多い。
2. 円の描き方
さぁさぁ、一息ついてね。メインは終わりであとちょっと、補足するだけ。
2章までで直線のパースはあらかた説明し終えただろう。しかし空間構成の過去6年中5年の問題は、円弧に代表される曲線が組み込まれている。むろん、円にもパースは乗る。これも正確に描けるようになりたい。

ベタなのは外接する正方形からばってんで中心→直径→接点をとってつなげる方法。しかし慣れてくると面倒くさいかもしれない。もう少し直接的な考え方もある。
円はどこから見ても円なので、ある種パースの枠を超越して捉えることができる。つまり、円を斜めから見ればそれは正方形の向き・形と関係なく必ずただの楕円であり(上図参照)、その長軸は円柱や円錐の軸と垂直になる(じゃないと回転したら形変わるので)。

そんなことを意識するだけで、直径と軸の長さからいきなり形を取れるんではないか。それだけ。
まとめ
だらだら1週間くらいかけて書いていたが、相応の情報量が盛り込まれた。理論はまだよくわからない人も、とりあえず大事な公式を確認しておいて。
・視線に対して垂直でない、平行な線の組は一つの消失点に収斂する
・地面に水平な線の消失点はアイレベル上にある
・視点がモノに近いほどパースがキツくなる
・円の長軸は軸と垂直
4つの文章が何言ってるかイメージできていればOK。あとは憶えて実用あるのみ。迷ったら全ての根本「視点から遠いほど小さく」に立ち返ろう。何も考えず呼吸するように形が取れるようになるまで、ひたすら思考回路を代謝しよう。一周した頃に、またこの記事を読んでみて。
参考:受験実用範囲を超えてパースの神になりたい人に、こういうコアなサイトもあるよ。パースフリークス
おまけ. パノラマパース
ここまでの話は全部ウソです。いや、表記するには便利な話だけど、地球を平面の地図にするような、厳密性を欠いた話なんだ。だって最初の図からおかしいんだもん。賢い人は引っかかってたよね?

隣車線まで行かずとも、直線の時点で正面から両側にパースかかるでしょ。両側に狭まっていくってことは、もはや直線ではいられないよね。

そう、特別な位置関係を除いて空間上の直線は視界ではビミョーに曲がってるはずなの。だったら道のラインももはや比率は一定じゃない。

一つの消失点から対極の消失点へ。全てが繋がった360°の景色の膜。伸縮する歪みがいざなうダイナミックな世界観。これがパースの本当の姿なのだ。
参考:パノラマパースの例




なぜ直線を直線で描くことに違和感がないかというと、ヒトの視界が切り取る部分がごく狭いからなんだ。スマホのカメラも射角たかだか60°で四隅を引き延ばして直線を直線に見せている。でもある程度の──ヒトも無意識で見えている全体くらいの──範囲を写そうとすると、じきに理想パースの限界が来て、パノラマの出番だ。100°〜、いわゆる魚眼というやつ。魚や草食動物に絵を描かせたらそれが普通。人間では首を振らないと意識できない範囲だけど、ひとつのコンセプチュアルな表現として成立するだろう。それでなくとも70〜90°くらいの広い範囲を描く場合、(3点透視の高さパースもそうだけど)隠し味的に仄かにつけるだけでも空間感が深みを増してくるからおすすめ。練習には広角のスケッチを。自然な曲げ具合を掴まないと、キモい絵になるよ。
以上、奥深いパースの原原原理から、"知っているとアド"レベルまで一気に話した。焦らず、わかる所からゆっくり咀嚼して、いずれはこれくらいの記事は書ける一年生になって来てね。じゃあまた、いつになるかわからんけど、次回の原論で。
(大西)